数学・物理 入門 微分方程式と力学系

問題
図のように、棒の端が床に対して、αの角度(ラジアン)で静止している。
この棒が、重力加速度gの下で、倒れる。
床は滑らかで、摩擦は無いと仮定する。棒の長さは２Ｌで質量はMとする。
棒の重心の運動を考えて、下記の値を求めなさい。
1) 棒の傾きがθの時の、回転の角速度と床からの抗力 R を式で表しなさい。
2) 棒の他端Bが床に着いた時の、角速度と点Bの速度を求めなさい。

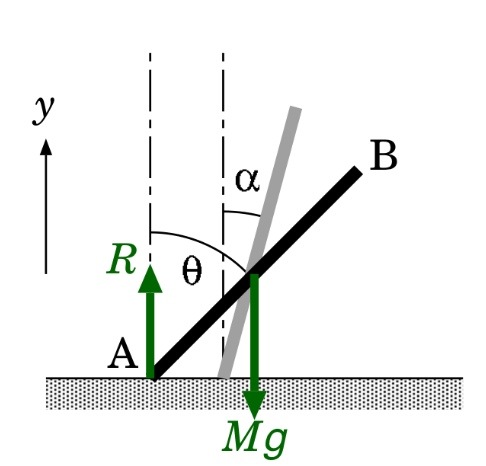
(何を学ぶか)
紙飛行機においても、飛行機は重心回りでピッチングとよばれる回転運動をします。また進行方向に、その方向の重力や抗力のバランスから並進運動を行います。重心回りの、回転運動と並進運動を理解するためにこの問題を考えましょう。

続きを読む →

縦方向の運動方程式

進行方向の力F (質量x加速度)は、推力-抗力、および重力の進行方向の成分で決まる。また、それに直交する方向の力Fは、揚力ー重力の成分 で決まる。

揚力、重さ、推力、抗力の釣り合いの式から、運動方程式が求められる。

釣り合い：機体全体の重心周りの（モーメント＝０）になる点
静安定：迎角変化に対する頭上げモーメント変化の大きさ（負ならば安定）

つまり，釣り合いはモーメントそのもの，安定はモーメントの変化率に注目しているとも言えます。

参考文献: F. Gavilan et al ,Output-Feedback Control of the Longitudinal Flight Dynamics Using Adaptative Backstepping ,Universidad de Sevilla,50th IEEE CDC & ECC, Orlando 2011
続きを読む →