剛体の運動は三次元空間では6自由度であり、重心等適切な代表点を決め、代表点の運動（移動）三次元とその代表点を中心とする回転運動（転向）三次元に分解して扱う事ができる。

飛行機の位置速度

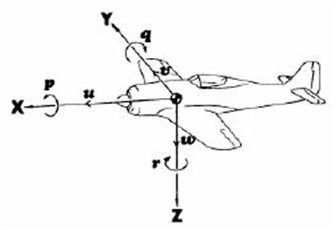
飛行機は右手系だ。フレミング右手の法則のように親指、人差指、中指を手の甲を上にし、それぞれ直角に突き立ててみよう。
このとき親指が機体の重心から機首に向かう軸つまりＸ軸を示す。同様に人差し指、中指が図示のとおりY軸Ｚ軸となる。それぞれ指の方向が＋だ。また指の方向の速度をuvwで表す。
各軸の回転角速度はpqrであり、親指から人差指、人差指から中指、中指から親指への回転方向を＋とする。

回転の表現:飛行機の姿勢
剛体が自由な回転運動をしているとき，剛体は重心を中心に回っていると考えることができます．つまり 自由な回転運動では，回転軸が重心を通る ということです．
3つの軸の中心を重心位置に置くことで、各軸を中心とした回転運動を表すことができる。3次元空間上では任意の回転は重心位置を中心とした3つの回転軸まわりの回転に分解できます。軸の選び方は独立なら任意です。
上のX軸と水平線のなす角度をピッチ姿勢、ピッチ角、機首姿勢などとよぶ。工学系ではθシータである。Y軸と水平線のなす角度がバンク角でφファイとする。Z軸はやっかいだ、水平線と比べるわけにはいかない。これだけはXY平面の今のX軸の方向を基準にして、そこからずれた角度をヨー角とか偏揺れ角などと云う。工学系ではψプサイである。

剛体の運動

剛体の運動は並進運動と回転運動の運動方程式を満たす。自転しながら公転している場合等、並進運動が回転運動の場合もある。その場合は並進運動も回転運動専用の式の方が適している。
剛体に働く力の合力が0で力がつり合っているとき、並進と回転の2つの運動方程式の右辺が0になり、剛体は等速回転しながら等速直線運動をしている。（それぞれ静止を含む。）

回転運動を記述するのには，回転の運動方程式というものが出てきます。並進運動の運動方程式 と同じ形で，F = m a という式が成り立ちます．並進運動の力 ，質量 ，加速度 に相当するのが，回転運動ではそれぞれ，トルク ， 慣性モーメント ，角速度 です．この慣性モーメントというのが，物体の回りにくさ を表す量です．

力のモーメント（ちからのモーメント、moment of force）は、力学における質点に回転運動を与える力のモーメントである。力の能率（ちからののうりつ）とも呼ばれる。単位は通常 ニュートンメートル(N·m)。とくに機械などの固定された回転軸において、回転軸のまわりの力のモーメントをトルク（torque）またはねじりモーメントと呼ぶ。