問題
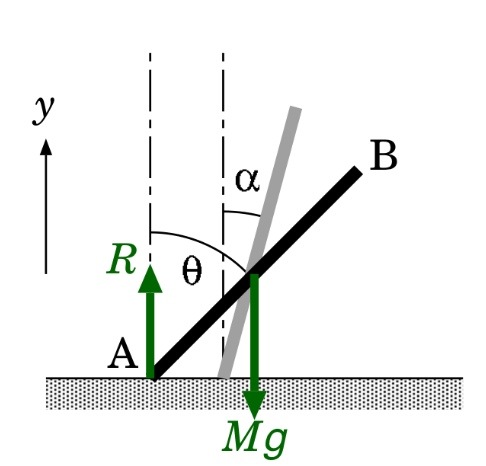
図のように、棒の端が床に対して、αの角度(ラジアン)で静止している。
この棒が、重力加速度gの下で、倒れる。
床は滑らかで、摩擦は無いと仮定する。棒の長さは2Lで質量はMとする。
棒の重心の運動を考えて、下記の値を求めなさい。
1) 棒の傾きがθの時の、回転の角速度と床からの抗力 R を式で表しなさい。
2) 棒の他端Bが床に着いた時の、角速度と点Bの速度を求めなさい。
(何を学ぶか)
紙飛行機においても、飛行機は重心回りでピッチングとよばれる回転運動をします。また進行方向に、その方向の重力や抗力のバランスから並進運動を行います。重心回りの、回転運動と並進運動を理解するためにこの問題を考えましょう。
ニュートンの第2法則は、併進方向の力 F =Ma の関係を表します。一方、回転運動では、トルク=力x回転中心までの長さ=慣性モーメントx角速度の変化率の関係式が使われますね。
(ヒント)
この問題は、回転運動と並進運動に分けて、現象の運動を表す必要があります。
1) 重心位置の併進・回転運動を考えましょう。
2) 初期条件は、t=0での角度と角速度の2つですが、角度はα、角速度は0です。
3) 拘束条件があります。それは、倒れるまで端の点Aが床から離れないという条件です。紙飛行機の場合は、この拘束はありません。
4) エネルギー保存の法則を使うことになります。この運動では、位置エネルギー、併進エネルギー、回転の慣性エネルギーの合計の総エネルギーが、初期条件の位置エネルギー(角度αで定まる一定値)と一致します。
・位置エネルギー=Mgh
・併進エネルギー=0.5M v^2
・慣性エネルギー=0.5I ω^2
回転運動をする物体の運動エネルギーは、慣性モーメント I と角速度 ω の2乗に比例する。
何故、エネルギー保存の法則を使うのでしょう。初期条件とその後の状態を、この場合はθ=π/2になった時の状態の関係式が必要になるからです。回転運動が無い場合を例に考えれば、高さhから落下運動する質量Mの物体が高さ0での速度Vは、 エネルギー保存の法則から、0.5MV^2=Mgh から V=√2ghと初期条件の関数として求められる。同様に、この問題でも初期条件であるαの関数で、床に落ちた位置での角速度などを求めるため、エネルギー保存の法則をつかいましょう。振り子運動の場合は、学んだように角加速度=√g/L・sinθの微分方程式になりますが、一般には解析解析が求められません。(θが小さい時解析的な解を求められます)。にもかかわらず振り子の最下点での速度は、エネルギー保存の法則から求められます。この問題も同様です。
5) 運動の状態を表すのに、状態変数があります。運動なので、時刻tで変わる変数です。時刻tの状態は、位置、速度などで表されます。回転運動があるこの問題では、拘束条件から、重心の高さはy=L・cosθとθであらわせるので、時間とともに変化する変数は、θとその変化率のみ考えれば十分です。角度θとその微分の角速度dθ/dt =ω が状態変数です。この二つの変数で、エネルギーを表現できますので二つで十分です。
6) この問題では、床の摩擦は無いので、重心は真っすぐ下方向の落ちます。もし十分な摩擦があれば、棒の端点Aは、動かないことになるます。
この場合は、拘束条件が代わり、重心は固定された点A回りの円運動をすることになります。拘束条件が変われば、この問題の答えも変わるでしょうか?考えてみましょう。この問題の方が簡単かもしれません。回転の中心が変わるので、慣性モーメントが変わります。重心回りで回転させるよりも、慣性モーメントが大きく回りにくいでしょう。これも考えさせられる問題ですね。
参考 棒の慣性モーメント
回転運動の仕事とエネルギー
回転運動における仕事とは 回転物体にトルクが作用して ある角度回転した場合 トル クの大きさと回転角の積で表わされる。 直線運動の場合と比較して説明すると 図に示すように 半径γのベルトプー・リの軸 にトルク T が作用した状態で 軸が角度ψだけ回転し 外周上の点Aが点Bへ距離 s だけ移動したとする。 この場合距離 sは s = rψ また 外周上に作用する力 F は F = T/r であるから仮想的に外周上にロープを巻いて これを 力 F で S だけ引いた場合を考えれぼ 仕事は すなわち E = Tψ したがって 回転運動においては仕事は トルクと回転角の積となることがわかる。 次に回転体の運動エネルギであるが 物体が運動しているとき エネルギ保存の法則により運動エネルギーをもつが これは運動の形態に関係なく 回転運動の場合にも回転運動のエネルギーを持っている。


