無風状態で飛ぶ凧の飛行原理
1.鷲鷹類の翼の形状に似たアスペクト比の高い平面形状を持つ翼

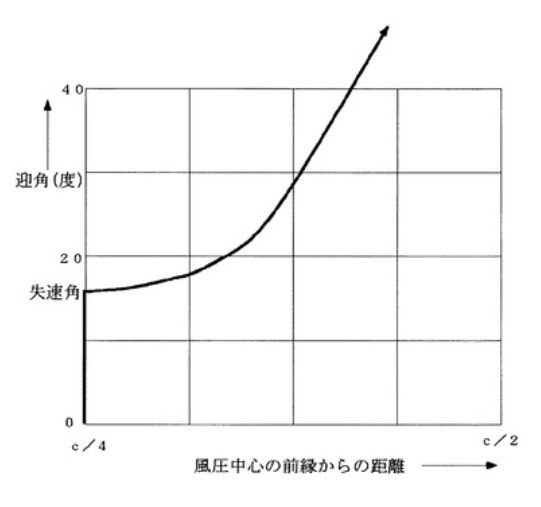
断面が平板の翼の迎角と風圧中心の関係を示したものである。
二次元平板翼の場合、風圧中心は、迎角が小さい(失速角以下)場合は、迎角の大きさにかかわらず翼の前縁から翼幅ｃの１／４の点にある。
この点で風に平行に翼を支えると、迎角にかかわらず翼には、翼の角度を変えようとするモーメントが変化しないので、風圧中心ともいわわれる。
また、この点では翼に加わるモーメントが常にゼロと一定であるので空力中心ともいわれる。(平板翼の理論より、空力中心と風圧中心が一致すること、さらに前縁から25%の位置の風圧中心があることが証明されている。)

一般に断面形状がキャンバーを持つ非平面翼では、モーメントはゼロではないが一定となる点がある。これが一般の空力中心といわれるもので、普通、空力中心と風圧中心は一致しない。

注意1 通常、航空機は、重心を空力中心よりも前にして飛行している。ノーズヘビイと言うが、頭を前に沈降させないために、尾翼に下方向の揚力を持たせ安定性と操縦性を確保している。

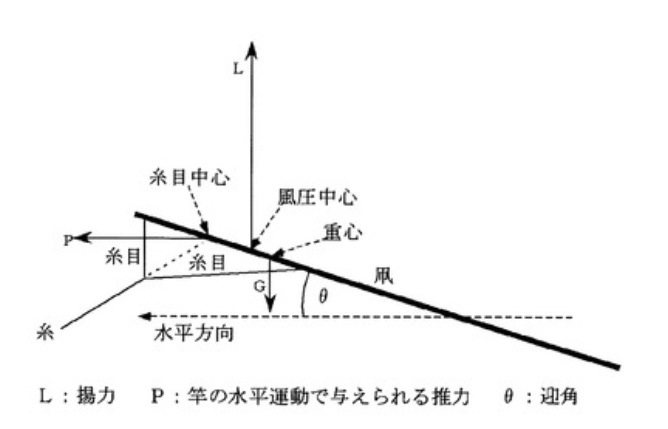
図は、凧が飛行中の力のバランスを示している。
凧重心は、凧の後端に調整可能な状態で置かれた錘位置の微調整で、航空機とは異なり、風圧中心、つまり、空力中心よりもやや後方に置かれている。
一方、竿と糸の水平運動によって糸目中心に加えられる推力Ｐが加えられるので、重心にかかる重力をＧとしたとき、迎角θが次の関係式で表される。
Ｔａｎθ＝Ｇ×（風圧中心～糸目中心間の距離）／（Ｐ×（糸目中心～風圧中心間の距離））ここで、この推力Ｐを調整することによって、迎角θを失速角以下の大きな値に保って、図に示すように大きな揚力係数が得られ、飛行速度が低くても効率よく揚力を発生して飛行を続けるようにすることができる。

このとき発生する揚力が重力Ｇよりも大きくなれば、凧は無風でも上昇することになる。また、ここで、竿を引くのを止めると、凧は自力で滑空しようとする。
凧の重心は、図に示すように、失速角以下の迎角θの場合の風圧中心よりやや後方にとってあるので、凧糸からの推力Ｐが反転する瞬間に生じる推力ゼロの瞬時の自力滑空では、重力Ｇに引っ張られて、凧は頭をもたげる。
その結果、凧は失速し、風圧中心が重心より後方に移動する。
すると、凧は再び頭を下げて非失速飛行することとなり、風圧中心が重心より前方に移動し、凧は再び失速状態になる。これをピッチング飛行という。
普通、ピッチング飛行では失速飛行時の抗力により滑空速度が極端に低下し、１～３回のピッチングで速度を失い墜落する。
そして、このピッチング飛行が持続する短い瞬間に竿を逆方向に引っ張ると、凧は糸目中心で引っ張られて再び非失速状態となり揚力を受けて上昇する。
このような竿の動きを繰り返すことにより、凧は無風にもかかわらず上昇していくものとなる。

以上の例では竿を使って手動で揚げた例であるが、おもちゃの電動自動車や電車を使って前進後退を繰り返せば室内の狭い空間でも小さい凧を安全に揚げることができる。