翼に働く力と作用点
揚力と空力中心
揚力は翼型(翼弦(翼を進行方向)に沿って切り取った型、AirFoil)によって生み出されるので、この翼型で考えてみましょう。 揚力は翼型に沿って様々に発生しているのですが、一般に迎角によって揚力の大きさやその主たる作用点が変わります。この作用点は「風圧中心」と呼ばれ、一般に迎角が小さければ翼弦の後方に、迎角が大きくなると翼弦の前方に移動します。 作用点が移動していると面倒なので、ある一点で考えられるようにしましょう。ある一点を中心にすると、風圧中心が移動することで揚力の大きさと風圧中心までの距離が変化することいなり、モーメントという距離と力の積算したもので考えることができます。
このモーメントは、先の平板翼の理論で示したように、揚力や抗力を表す式と同じように、次で示すことができます。
モーメント(M) = cm(モーメント係数) × 1/2 × ρ(空気密度) × v2 × S(翼面積)× C(翼弦長)
一般に迎角を変化させると、モーメントが増減します。モーメントが増減するということはモーメント係数が変化することですが、迎角が変化してもモーメント(=モーメント係数)が変化しない点があります。 この点が「空力中心(ac,Aerodymaic Center)と呼ばれる点です
この点では迎角によっても翼自身の釣り合いが取れていますので、つまり、この点に揚力が作用していると考えることができます。
平板翼の理論のとおり、空力中心は厚翼を除いたほとんどにおいて、翼型によらずに翼弦の25%近辺にあります。
そして、空力中心も風圧中心も同じ翼弦の先端より25%の位置にあります。
平板翼の場合に空力中心と風圧中心が一致するからと言っても、一般の翼では一致しません。本来この2つは明らかに区別されるべき物であり混同してしまうと、揚力はいかなる時も空力中心に働くという誤解を生みかねないし、またそう曲解してしまうと空力中心でのモーメントはゼロという本末転倒な結論を導きかねません。
普段、一般の人が頭の中で容易にイメージされる揚力作用点は「風圧中心」です。つまり翼に働く力の実際の作用点のことを「風圧中心」といいます。
ところがこの点を基準にして計算をしようとすると結構な問題があるのです。
風圧中心は翼の迎角に応じて大きさ・方向・作用点の位置が色々と変化してしまうのです。
風圧中心は迎角が小さい時は翼の後方に、大きくなると前方に移動しています。力とモーメントを迎角変化のその度ごとに計算することはかなり面倒です。
もう少し計算に適した点を考える必要があります。
この問題を解決するための点が「空力中心」です。この点は翼の前縁から1/4の場所にあり、この点まわりのモーメントは迎角の変化に関わらず常に一定というとても都合のいい点なのです但し注意しないといけないこともあります。
空力中心では迎角によるモーメント変化率がゼロですが、モーメントがゼロというわけではありません。
その点まわりのモーメントがゼロなのは
「風圧中心」です。(迎角変化で位置は変わりますが)
重心と機体の回転運動
機体の回転軸の中心は、重心位置です。
風圧中心は揚力の作用点ですので、そこに上向きの力が働きます。重心にはその逆に常に下向きの力が働きます。 空力中心と重心が一致していれば、力の作用方向が相反しますので釣り合うことになります。ただ、この2つが一致していると厄介なことになるのです。
前に「静的安定性は突風とかの外乱等があった時に元の姿勢に戻ろうとする性質」と説明しましたが、重心と空力中心が一致している時に上向きの外乱を受けた時、どうなるのでしょうか。
外乱によって頭上げの力が働くと、迎角が増えて揚力が増加します。ただ、空力中心と重心が一致していると揚力が増えても重量は変わりませんので頭上げの力を打ち消すことができません。
つまり、受けた頭上げの力は重心から見て頭上げのモーメントになりますので、増えた揚力が重心にとって頭下げモーメントになる関係があれば、釣り合う(相殺する)方向にすることができます。
このことは空力中心と重心の位置関係を暗示しています。
「増えた揚力が重心にとって頭下げモーメント」として働くには、「重心は空力中心より前にあること」になるのです。これが縦の安定性の条件です。
紙飛行機の場合、三角翼でかんがえれば、アスペクト比の小さい場合、言い換えれば、より鋭角の細長い翼場合は、重心位置は空力中心よりもうんと前になります。逆に、スカイキングのような鈍角で幅広いアスペクト比の大きい紙飛行機の場合、重心位置と空力中心は、近くにあります。
前者の細長い紙飛行機は縦の安定性は良いですが、逆に翼面積が狭くなり揚抗比が小さく、放物線のような飛行になるという欠点があります。スカイキングのような紙飛行機は、重心位置と空力中心が近く、翼面積を大きくとれるので、揚抗比が大きくなって遠くまで飛ばせるでしょうが、縦の安定性の調整が重要になります。
翼の重心と空力中心の算出方法
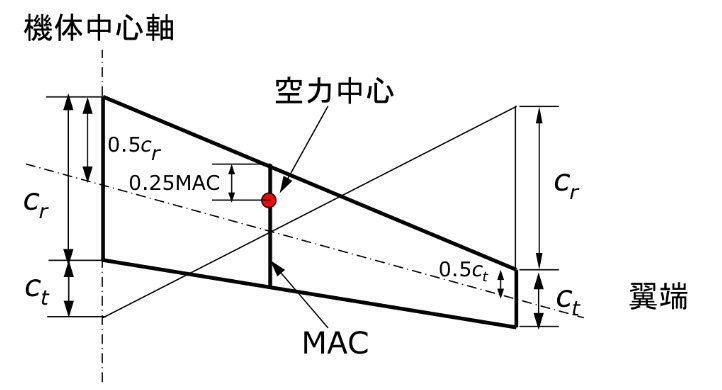
主翼空力平均翼弦 (MAC = Mean Aerodynamic Chord)が重要です。
空力平均翼弦(MAC:mean aerodynamic chord)
実際に翼が発生させる揚力は翼幅方向に変化するが,翼全体を通じてある代表的な翼弦を想定し,この翼弦の位置に揚力がすべて作用すると仮想すれば,翼の特性を計算する場合便利となる。この仮想上の翼弦を空力平均翼弦と呼び,翼幅方向の位置および翼弦長は,空力平均翼弦(MAC)として求めることができる。
おもな旅客機の主翼の空力平均翼弦長は,
737-400 134.46in(約3.42m)
747-400 327.78in(約8.33m)
777 278.52in(約7.07m)
エアバスA310 214.2in(約5.44m)
ダグラスMD-11 295.78in(約7.51m)
また、MACは、機体重心位置だけではなく、飛行機設計に必要な”尾翼容積係数”機体重心位置を決めるに当たって、MACを出さなくてはなりません
主翼は特殊な物を除いて、胴体中心線を境に左右対称です。ですから、片方の翼でここからは考えていきます。
まず、紙と鉛筆と定規があればできる、作図による求め方です。
ごく普通のテーパー翼を例題にします。
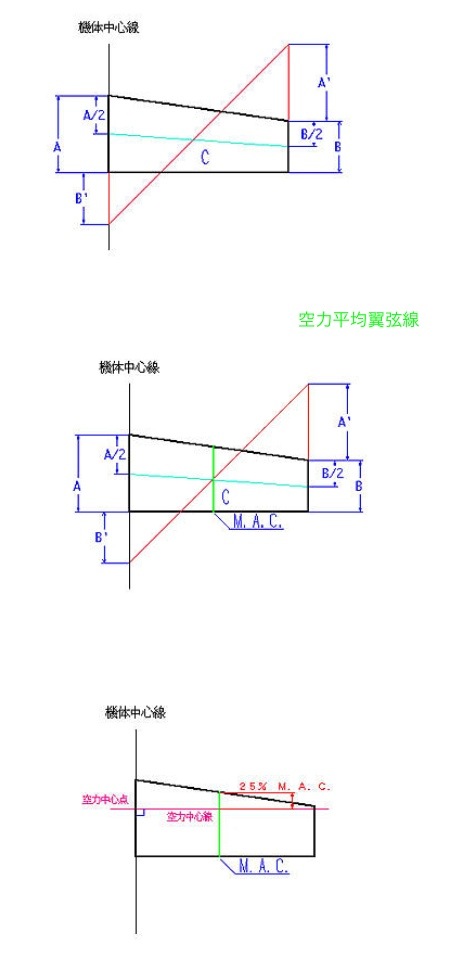
1 任意のテーパー翼平面図を書き、ここでは、最大翼弦をA、
最小翼弦をBとし、おのおのの中点を線で結びます。
2 翼端の前縁から前に向かって最大翼弦Aと同じ長さの線A’を引き、
翼中央の後縁から後方に向かって最小翼弦Bと同じ長さのB’を引いて、
おのおのの先端を結ぶ線を引きます。(赤い線)
水色と赤い線の交点をCとします。
3 交点Cを通る翼弦線を引きます。
この線が、(グリーンの線)空力平均翼弦線です。
4 前縁から、MAC上の空力平均翼弦長の25%の位置に点を打ち、
そこから、機体中心線に垂線を引きます。
機体中心線と、この垂線の交点が、空力中心点であり、
この垂線が空力中心線です。
機体の重心は、スケール機や練習機などひっくり返ったり、無茶なロールをしない、安定性を求めるタイプの飛行機であるならば、15~25%MACあたり、ひっくり返ったり、アクロを望むならば、運動性重視の20~35%MMACに設定するのが一般的です。
単純なテーパー翼、デルタ翼、後退翼などは、この方法でほとんど対応できます。
ところで、楕円翼、ダブルデルタ翼、鳥の羽のような翼、こういったタイプの物は、作図法では、対応が難しくなります。
では、どうしましょう?
作図法で出した、C点は、なんだと思いますか?
実は、その平面図形の重心点なのです。(機体の重心と混同しないように)
とすれば、平面図の重心点を通る翼弦線がMACと言い換えることができます。
最近のCADには、たいてい2次元解析の機能が付いています。
これを使えば、ある平面図の面積、重心点座標など、コマンド一発で出ます。
重心点が出れば、その点を通る翼弦線を引けば、MACが求められます。
どんな主翼平面形でも、ダブルデルタだろうが、鳥型だろうが、楽勝です。
なお、”翼弦”は機体中心線に平行に引きます。
では、CADを持っていない場合はどうしましょう?
ともかく平面図の重心が見つかれば、いいんですよ!
糸とセロテープをつかって、その翼をつり下げ、
翼が水平になる糸の取り付け位置、すなわち重心を探るのです。

1件のコメント
コメントをどうぞ →